An Original Formalism

The MODL approach is an essential component that gives Khiops three significant features: a natural resistance to overfitting, no need to optimize hyperparameters and impressive scalability. However, what is the MODL approach? How does it distinguish itself from standard machine learning approaches?

This section introduces and compares MODL with conventional approaches. Exploring this scientific framework is a crucial point, as it fundamentally influences the functioning of Khiops. A deeper understanding of this original formalism will highlight the unique features that set Khiops apart in the machine learning landscape.

Standard Machine Learning Approaches

Most machine learning approaches are derived from statistical learning theory. This section shows how these approaches rely on optimization of hyperparameters to limit overfitting, and how Khiops contrasts with them. Indeed, Khiops is freed from the complexity of hyperparameter optimization, which offers a significant advantage over other machine learning approaches.

A Closer Look at Empirical Risk Minimization

In the field of machine learning, the goal of learning algorithms is to identify the optimal model, represented as \(\hat{h}\), from a set of possible models, denoted as \(\mathcal{H}\). This identification relies on a sample of training examples, denoted by \(\{(x_i,y_i)\}_{i \in [1,n]}\), with each example associating input variables \(x\) with their corresponding ground truths \(y\) to be predicted.

For any given training example, a loss function, \(\mathcal{L}(h(x_i),y_i)\) (or cost function), is used to evaluate how the predicted output of a model \(h(x_i)\) compares with the actual ground truth \(y_i\), i.e., the expected value. The loss function thus evaluates the relevance (or the cost) of a candidate model \(h\), for the example \((x_i,y_i)\). A popular choice of a loss function is the squared error, defined as \((y_i - h(x_i))^2\).

The average value of the loss function given all the training examples \(\{(x_i,y_i)\}_{i \in [1,n]}\) is the empirical risk. Under the assumption of independence and equal distribution among the training examples, this empirical risk provides an approximation of the actual risk the model will face when dealing with new data, corresponding to the mathematical expectation. For instance, using the squared error loss function, the associated empirical error is defined as \(\frac{1}{n} \sum^n_{i=1} (y_i - h(x_i))^2\). This is known as the method of the Least squares.

The concept of empirical risk might suggest that a model that correctly explains the training examples and minimizes the empirical risk would be an ideal one. However, an exclusive focus on minimizing the empirical risk can lead to overfitting, where the model doesn't generalize well to new data. To address this, most machine learning approaches use a regularization term, \(Reg(h)\), as part of the optimization criterion:

\[\hat{h} = \arg \min_{h \in \mathcal{H}} \left [ \underbrace{\frac{1}{n} \sum^n_{i=1} \mathcal{L}(h(x_i),y_i)}_\textrm{Empirical risk} + \gamma . \underbrace{ \vphantom{\sum^n_{i=1}} Reg(h)}_\textrm{Regularization} \right ]\]

The regularization function, \(Reg(h)\), can take various forms. However, its purpose remains constant: to impose a penalty on excessively complex models to prevent overfitting.

The Fundamental Role of Hyperparameters in Scalability

Looking at the equation presented above, it is clear that the empirical risk and regularization terms don't share the same mathematical nature. That's why the regularization strength \(\gamma\) is introduced to balance the training objective between empirical risk minimization and regularization. However, the learning algorithm on its own cannot determine the best value of \(\gamma\) as it comes under the umbrella of model selection (see Hyperparameter).

This issue necessitates a trial-and-error process, which involves validating possible values of \(\gamma\) and assessing the candidate model \(h\) using a dedicated validation set of examples. This process is typically repeated multiple times for robustness against sampling variation, a method known as cross-validation.

In real-world applications, standard machine learning methods don't have just one, but numerous hyperparameters, the optimal values of which can't be figured out by the learning algorithm itself. These hyperparameters may include the depth and minimum number of examples in the leaves for decision trees, or the number of layers, the size of layers, and the transfer functions for neural networks.

To discover the best set of hyperparameters, it's necessary to test all possible combinations using a method called grid-search. However, the number of hyperparameters directly impacts scalability since it determines how often the learning algorithm needs to be executed. For instance, if a grid search tests five candidate values for each hyperparameter over a ten-fold cross-validation process, the training algorithm will need to be repeated:

• 250 times for 2 hyperparameters,
• 1250 times for 3 hyperparameters,
• 6250 times for 4 hyperparameters,
• 31250 times for 5 hyperparameters, and so on.

Standard approaches are limited in their scaling by the empirical optimization of hyperparameters, which remains necessary to fight against overfitting.

Khiops

Khiops operates on a different paradigm from conventional machine learning approaches, which focus primarily on minimizing empirical risk. It uses the MODL approach, which is based on a Bayesian model selection principle. This approach gives Khiops an advantage, freeing it from the constraints of optimizing hyperparameters and enhancing its robustness against overfitting. The following discussion clarifies the underlying principles of the MODL approach, drawing attention to its inner workings and the benefits it brings to machine learning.

A Bayesian Model Selection Approach

The MODL approach aims at selecting the most probable model given the training data. The Bayes formula is thus the starting point for deriving the optimization criteria used, whose general form is the following:

\[\arg \max_{h \in \mathcal{H}} P(h|d) = \arg \max_{h \in \mathcal{H}} \frac{P(h)P(d|h)}{P(d)}\]

where \(h\) represents the model at hand which belongs to \(\mathcal{H}\), the set of learnable hypotheses, and \(d\) is the training set.

All the MODL optimization criteria are designed in the same way (optimal encoding, feature engineering and parsimonious training), through the following steps:

• definition of the family of models \(\mathcal{H}\), i.e. the model parameters, with respect to the learning task to be addressed;

• definition of the prior distribution \(P(h)\) over these parameters, which is always hierarchical and uniform;

• obtaining the optimization criterion from the development of the Bayes' formula by accounting for the likelihood term \(P(d|h)\);

• model training by optimizing the final criterion just once.

Link with Information Theory

In Information Theory, the model selection problem described above can be translated into an encoding problem, whose purpose is to find the most compact way of encoding an information source for transmission over a telecommunication channel. Let's consider an information source emitting symbols [e.g. a, b, c, etc.] whose alphabet is known. In information theory, the negative logarithm of the probability that a symbol is emitted [e.g. \(-log(P(a))\)] represents its optimal coding length, denoted by \(L\) and expressed in bits. According to Shannon's intuition, the most efficient encoding strategy assigns a short coding length to the most frequent symbols.

In the same way, the probabilities in Bayes' formula above can be replaced by negative logarithms to obtain a MODL criterion to be minimized, that can be interpreted as follows:

\[-\log(P(h).P(d|h)) = \underbrace{L(h)}_{\textbf{Prior}} + \underbrace{L(d|h)}_{\textbf{Likelihood}} \]

• the prior corresponds to the coding length of the model, i.e. the number of bits needed to describe it;
• the likelihood is the coding length of the training data, with the model in hand.

In this encoding problem, the model is transmitted over the telecommunication channel first, followed by the training data. The Minimum Description Length (MDL) principle aims to select the most compact model describing the data, and it is applied in the MODL approach by the choice of a hierarchical prior representing successive choices on the model parameters.

Let's Dive Deeper with the Analogy of Density Estimation

To illustrate the model selection performed by Khiops, we draw an analogy with a very simple problem: estimating the density of a numerical variable using histograms. Here, the histogram takes on the role of the model under training. This is a discretization model (i.e. dividing the domain of the variable under study into intervals of varying size) that is instantiated by first defining the number of intervals, then the frequency and bounds of each interval. For the sake of illustration, consider a dataset drawn from a Gaussian distribution.

The MODL approach selects the most probable model based on the data, among all possible models, i.e. histograms with a more or less important number of intervals, and varying interval sizes. As shown in the following figure, the key is to choose the right number of intervals. An insufficient number of intervals leads to oversimplification and thus to a loss of information. Conversely, an excessive number of intervals introduces unnecessary complexity and sensitivity to outliers and noisy values.

In the MODL approach:

1. the Prior \(P(h)\) specifies a preference for the simplest model;
2. the Likelihood \(P(d|h)\) measures the model's ability to accurately describe the data sample.

The following paragraph presents the role of each of these terms and how they are constructed:

• The Prior follows a particular form - hierarchical and uniform. In our histogram example, the parameter hierarchy has two levels: (i) the choice of the number of intervals in the histogram; (ii) the definition of the bounds' positions. Model instantiation involves successive choices of parameter values by moving towards the bottom of the parameter hierarchy (first the number of bounds, then their positions). All possible choices have the same probability within each hierarchical level, preserving neutrality in model selection and allowing data to best express their information. The hierarchical form of the prior limits the complexity of the model, reducing the risk of overfitting. Indeed, increasing the number of intervals in a histogram considerably increases the number of possible positions for its bounds, making it less probable a priori.

• The Likelihood plays the opposite role, favoring models that describe the data sample as accurately as possible.

During training, optimizing the MODL criterion selects the most probable model by combining the Prior with the Likelihood, thus achieving a balance between underfitting and overfitting.

What you should remember

Unlike conventional approaches, no weighting of the regularization term (the prior in this case) is necessary, as the mathematical consistency between the prior and the likelihood follows from Bayes' formula. This explains the absence of hyperparameters in the MODL approach.

Conclusion

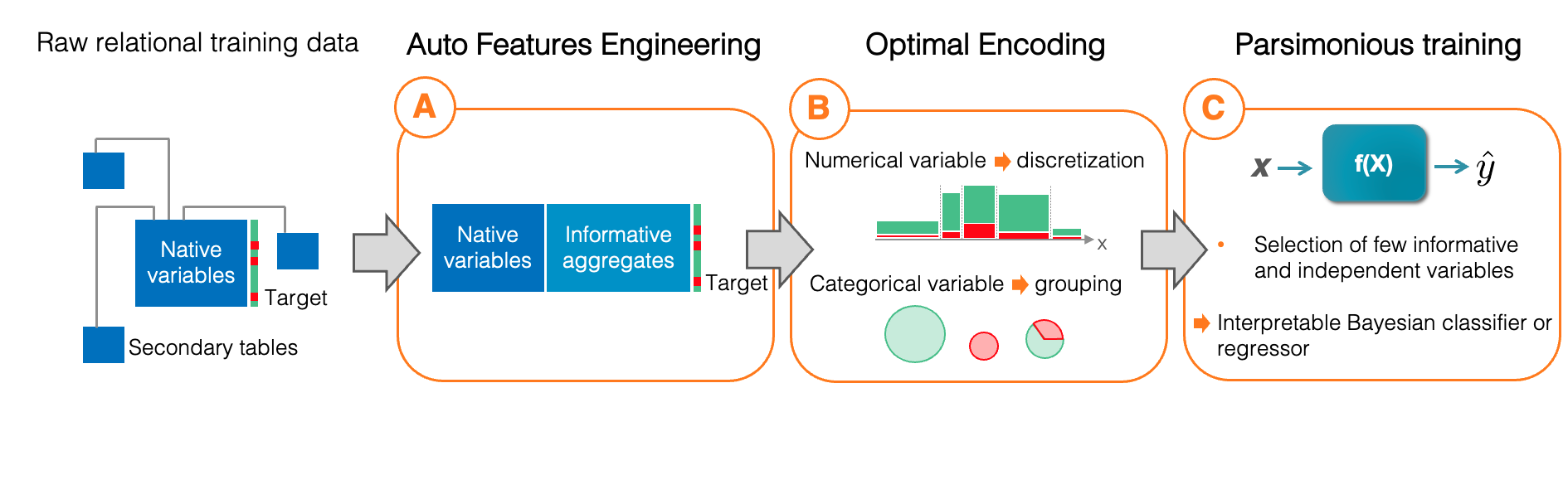
The MODL approach is rooted in both Bayesian and Information theories. What makes Khiops original is the end-to-end application of the Minimum Description Length (MDL) principle across the entire AutoML pipeline provided, with a focus on industrial-strength scalability. As a result, all the learning algorithms used by Khiops share the following special features:

1. Trained models consistently generate a segmentation of the data (e.g. the histograms described above discretize the variable to estimate its density). The structure of this segmentation varies according to the specific learning task at hand, within the AutoML pipeline:

   • Discretization of numerical variables consists in dividing their range into several intervals;
   • Grouping of categorical variables involves merging some of their modalities;
   • Variable Selection during Parsimonious Training discriminates the relevant variables from the irrelevant ones.

   After this partition has been trained, the statistical models that Khiops generates take the form of a piecewise constant estimator. This means that within each segment of the partition, the model predicts a constant value (e.g. as inside a histogram interval).

2. During training, the most probable model given the data is selected. This selection is based on MODL optimization criteria, which are derived from Bayes' formula, exploiting a unique form of prior distribution. The choice of a prior that is hierarchical and uniform at each level of the hierarchy comes from the principle of minimum description length (MDL) in information theory, and corresponds to the most compact way of describing the model.

3. By design, the optimization criteria prevent overfitting, thanks to (i) the specific shape of the a priori distribution, which favors simpler models, and (ii) the cardinality of the model family, which increases with the number of training examples. These two mathematical features automate the balance between model accuracy and robustness. As the size of the training set increases, the likelihood term gains more weight, enabling the model to become increasingly accurate while maintaining its robustness (this intuition is detailed on the discretization section).

4. Khiops algorithms require no hyperparameters, as all parameters defining the model are optimized by the optimization criteria. This eliminates the costly step of empirically optimizing hyperparameters. What's more, the algorithms are designed to handle large amounts of data and adapt their operations to the available hardware resources.

In essence, this is the crux of Khiops' secret, implementing the MODL approach across all stages of its AutoML pipeline (Stages A, B, and C). This enables the learning algorithms to accomplish their tasks in a single run!